文章主题:金融交易策略, 特征重要性, 机器学习模型, 数据挖掘
这篇文章比较technical,来看故事的同学请直接忽视。想了解怎么开发金融交易策略的,可以继续。
在探讨量化交易策略的过程中,我们通常会遵循以下步骤来开展研究:首先,我们会收集一系列具有预测性的数据,以期从中挖掘出潜在的投资收益α值。接着,我们会利用这些α值来训练各种预测模型,以便对未来可能的投资回报进行预测。在完成模型的训练之后,我们会在实际模拟的基础上进行多空策略的回测,以检验其性能表现。一旦回测结果满意,我们就有望将这一策略应用到实际交易中,从而获得更高的投资收益。
在我们的团队中,有越来越多的金融机器学习模型开始不依赖于回测夏普比率、最大回撤以及其它指标了。
对于有经验的参与者而言,也许你已经意识到了这一点:回测作为量化金融领域的基础性任务,虽然重要却并非完美无缺。在进行回测之前,我们会对隐藏在其中的机器学习模型及其关键特性进行深入的剖析。
《Advances in Finance Machine Learning》一书的作者Marcos Lopez de Prado身为康奈尔大学工程学院的客座教授,在他的著作中对这一观点进行了阐述:回测并非研究手段,而特征重要性才是关键所在。

这篇文章主要针对《Advances in Finance Machine Learning》中涉及的一些方法和实验进行深入探讨,以揭示特征重要性在研究交易策略中的重要性和实际应用价值。
为什么不相信回测了呢?策略算法工程师在做研究时,往往把假设陈述为 “基于特征X和模型Y的策略会得到夏普比率Z”。然而,研究是要形成关于金融变量之间因果关系的假设。回测只是验证已确认的假设的商业价值的工具之一。由于经典的回测是在历史数据上进行的,所以我们倾向于解释过去模拟交易的随机模式和相关性(不能解释因果关系)来证明假设。之后,基于这些“发现”,会多次“修正”模型和策略,这就导致了下一个问题。回测容易出现多重假设测试——越是试图基于单一数据的回测来优化策略,就越有可能深陷错误的发现。因此,“过度拟合”的预测模型很容易在回测中表现良好,但我们绝对不能把钱放在这样的模型上。在本文中,我们将探讨如何在无需回测的情况下评估基于多个数据源的交易策略。这一方法不仅适用于机器学习领域专业人士,同时也为检验交易及投资组合管理指标以外的策略或假设提供了实用框架。
采用特征重要性有哪些显著的优势
除了与研发相关的主要优势外,还有其他几个对金融机构非常有利的优势。在实际应用中,我们可以通过运用特征重要性分析的方法,以期达到理想的效果。
在评估新的数据源、市场和替代数据研究时,正确的特征重要性对于识别哪些数据具有真正的预测价值至关重要。在实时交易中,只选择最重要的特征进行交易,可以作为降低机器学习模型性能下降相关风险的方法之一。跟踪特征重要性在时间上的演变,可以比传统的计量经济学模型更好地解释经济因素的动态,这也有利于风险管理和早期趋势预测。特征重要性
统计学中著名的p值并不是验证特征重要性的完美方法。下面是在研究中可以用到的一些方法:
单一特征重要性法(SFI,Single Feature Importance)是一种适用于各类模型的方法,它采用OOS(out-of-sample,样本外)的方式对各个变量进行分析。这种方法的特点在于,它会逐一评估每一个特征的重要性,从而找出对模型预测结果影响最大的因素。然而,在某些情况下,该方法可能会遇到一些问题。例如,当某些特征之间存在相互依赖关系时,仅凭单一特征的重要性法可能无法准确判断其重要性,因为它只考虑了特征本身的影响,而忽视了与其他特征的相互作用。此外,当特征的重要性取决于其他特征的出现情况时,该方法也可能会出现问题,因为它的评估是基于每个特征单独的重要性进行的。
MDI(平均不纯度下降法)是一种针对树形算法的优化方法,主要用于处理样本内的数据。通过该方法,可以有效地降低数据的不纯度,从而提高模型的性能。由于其独特的设计,MDI在处理大规模数据集时表现出较高的效率,同时保持了良好的可解释性,这使得它在实际应用中具有很大的价值。
平均准确度下降法(MDA,Mean Decrease Accuracy):OOS样本外计算,适用于任何模型,最重要的是,它直接比较了将某特征进行无序打乱前后,训练结果的评价指标准确度的下降情况。另外,还有更高级一点的方法。
聚类特征重要性:当两个特征共享信息时,在MDA中打乱数据可能会导致性能降低,因此,采用聚类的方法是有意义的。
SHAP(SHapley Additive exPlanations):(以一种统一的方法来解释任何机器学习模型的输出。)是一种解释个体预测的方法。SHAP是基于博弈论最优的Shapley值,它在现代机器学习实践中应用非常广泛。最后,我们希望能够有一种方法来检验发现的重要特征的正确性是否“充分”。这个可以借助PCA来实现,PCA是无监督的,因此,不会对标签进行过度拟合。还可以通过计算PCA“特征重要性”(即特征值大小)与其他任何特征重要性方法之间的 “相关性”(加权Kendalls tau)来实现。
交叉验证
对于大部分的特征重要性,我们都需要训练模型并评估其准确性,所以我们需要一种方法来正确测试这种准确性。典型的组合方法是K-Fold交叉验证和时间序列交叉验证。
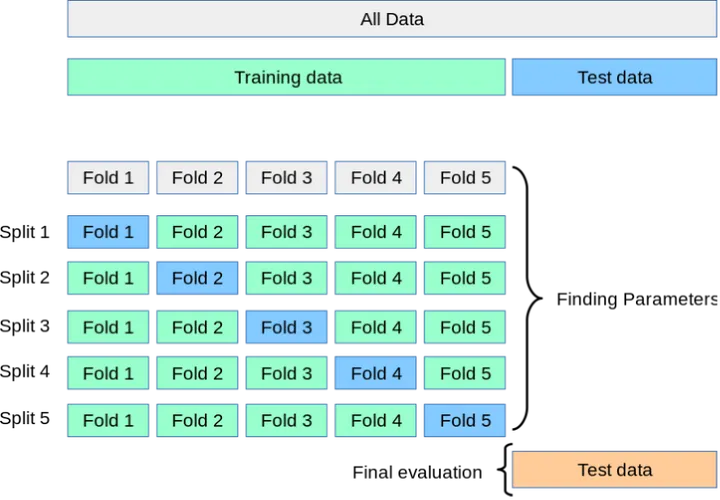
在金融领域,由于各种原因,比如不是IID采样得到的观测值或样本数量不充足等,为了充分利用数据集对模型或算法效果进行测试和评估,需要更严格地分离训练集和测试集。一个简单的K-Fold交叉验证示意图如下所示:
模拟数据实验
首先,为了评估整个流程,我们可以用模拟数据进行二元分类实验,其中一部分特征是预测性的,一部分特征是冗余的(即只是预测性特征的组合),还有一部分特征是完全随机的。特征重要性的目标是告诉我们哪些特征是不重要的,所以我们在模拟交易中只能依靠真实的”阿尔法”。
为了更接近交易场景,可以做一个信噪比很低的数据集:3个信息特征、2个冗余特征和15个随机特征,分别表示为 “I”、”R “和 “N”。下面就来看不同的特征重要性算法的结果。
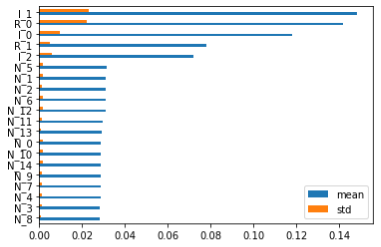
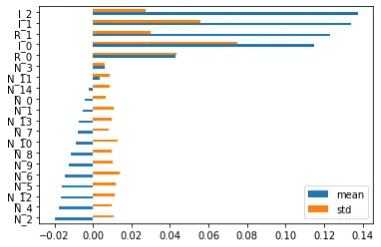
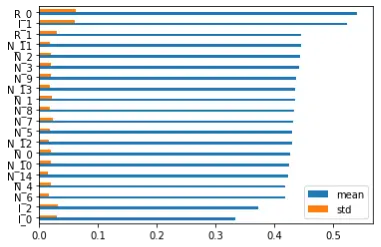
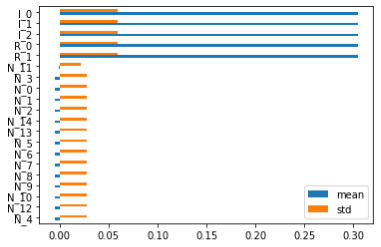
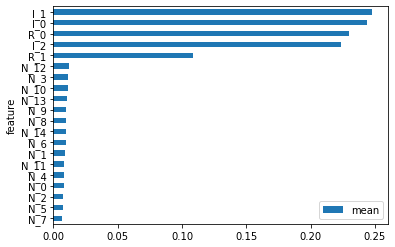
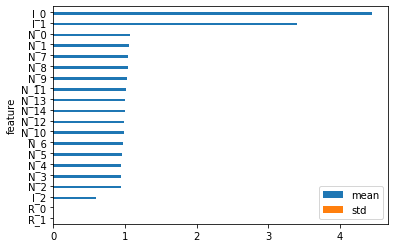
从视觉上看,除SFI外,其他方法在识别 ” I “和 ” R “特征方面都表现良好。另外,PCA特征值和CFI重要性之间的加权Kendalls tau计算出来为0.44,表现出了较高的相关性。
市场数据实验
下面来看真实的金融时间序列来做的重复实验。数据选取的是2000年到2020年的AAPL。首先,用分数阶微积分使时间序列平稳,提取以下特征数据集。
5个统计特征:均值、标准差、偏度、峰度、收盘价非整数差分的自相关性。5个交易指标:RSI、OBV、ATR、Hilbert变换周期和相位;5个随机 “特征”:正态分布、均匀分布、二项式分布、泊松分布和逻辑分布,这些分布将代表不同来源的非信息特征。接下来,用三重界限法标签(triple barrier labeling)创建二元分类标签。特征的滚动窗口为14天,预测范围为7天。在这种情况下,特征重要性将如何表现呢?下面是基于2000年到2010年的数据得到的特征重要性,然后,用2010年到2020年的不同特征数据集测试 “样本外”数据的性能。
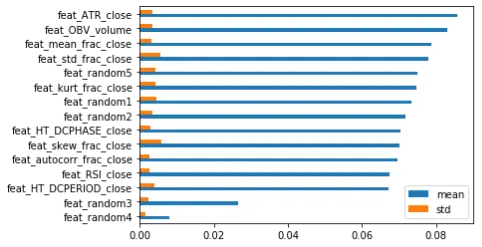
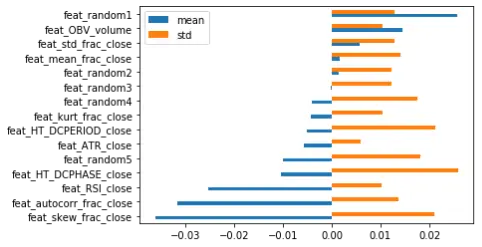

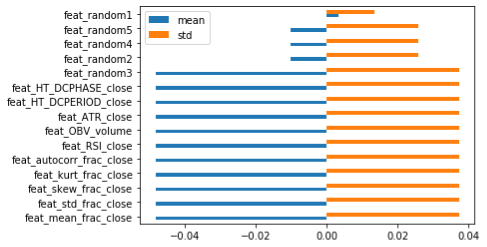
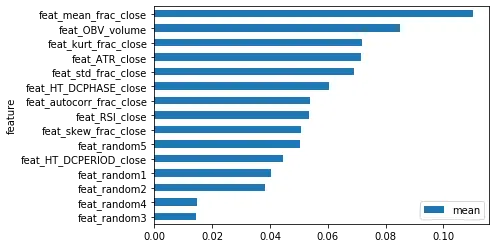

可以清楚地看到,所有的方法都至少给了一些随机特征很高的优先级。
虽然这些表现并不完美,但至少可以除去大部分的垃圾特征,降低未来的风险。另外,还可以用其他类似的数据集中检验特征重要性,如MSFT(微软)和IBM。下面分别是MDI、MDA和SHAP可视化的结果。
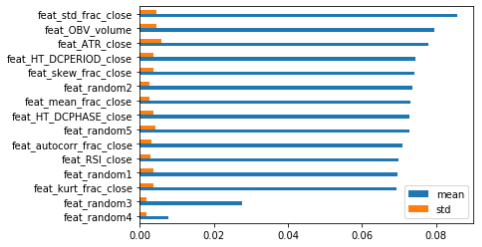
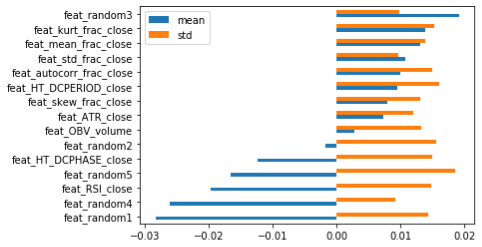
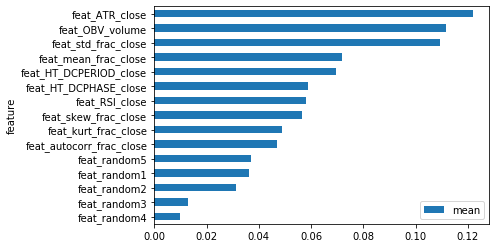
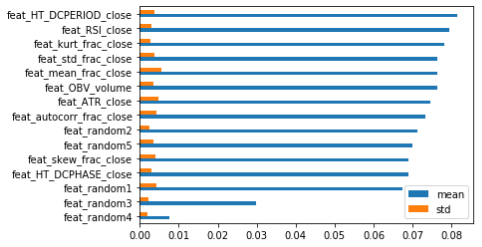
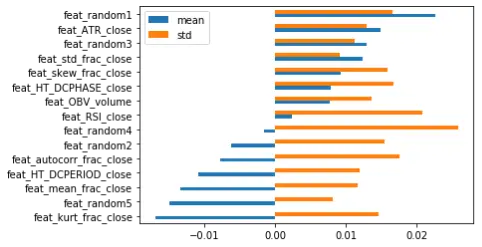
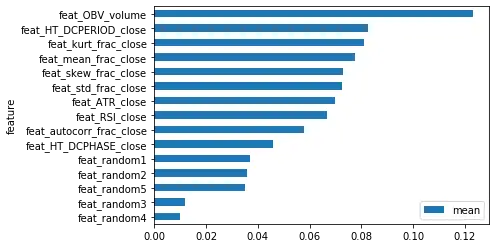
根据这三个数据集排名前5的SHAP值,可以选择以下几个最重要的特征。
然后只在样本外数据上进行Purged K-Fold交叉验证,计算几个指标。由于随机森林算法的核心中使用了Bootstrapping算法,所以不同的运行结果可能会有所不同,可以进行100个实验,将其做平均,计算出F1分数、马修斯相关系数和ROC-AUC等指标。
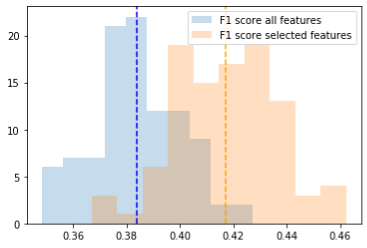
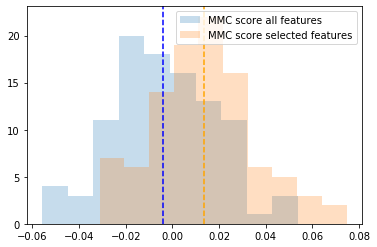

从上面的结果可以看到,平均来说,在样本内精心选择的特征集上训练的模型,在样本外的表现更好。
Numerai数据实验
Numerai是一家使用AI技术的金融技术公司,以举办去中心化金融预测挑战赛(类似于kaggle)寻找最佳交易策略闻名。用户获得经过模糊和匿名的金融数据,创建并提交模型,之后将这些模型组合成一个元模型,在真实市场上进行交易。基于这个元模型的贡献及其在真实交易中的表现,用户可以获得相应的报酬,报酬可能是美元或加密货币。
Numerai数据的一个问题是我们对数据和标签一无所知:名称标签和分类都被加密了,并且在每个时间段内(不同的年代era)特征都会变化和调整,这里无法应用任何金融知识来获得最大的利益。
可以做的是对XGBoost的超参数进行调整,下面来看看特征重要性分析是否能在这方面起到作用。

如果年代其实也是混杂的呢?那最好做正常的分组K-Fold交叉验证,年代对应分组。另外,为了加快计算速度,这里使用了线性回归模型,只使用MDA作为训练数据的特征重要性分类器。

下面来选择最重要的特征。Numerai数据集中的特征被分为6类:
feature_charismafeature_constitutionfeature_dexterityfeature_intelligencefeature_strengthfeature_wisdom根据MDA特征重要性,从每一类中选取前75%来保存一致性,并在样本外数据上进行交叉验证实验。这里的直方图代表了验证数据集上的不同年代。所有情况下的ML模型都是简单的线性回归。



从上面的图中又可以看到,在”更干净”的数据集上训练出来的模型,即使不知道每个特征的含义,单纯依靠 MDA的值,也比在完整数据集上训练出来的模型表现更好。
我们没有参加比赛,不知道它的实战表现如何,但这已经是一个很好的开始了。
结论
我们可以看到,为了形成我们对金融市场的假设或策略并对其进行评估,确实需要机器学习的过程和研究特征重要性。当我们要定义实际的交易和风险管理规则时,回测可以后面再做,但在思考新的变量、新的因子或新的阿尔法来帮助我们战胜市场时,回测在这个阶段并不是一个非常理想的方法和步骤,而特征重要性也许是一个更好的选择。
可以看到,机器学习模型的特征重要性可以帮助我们识别出真正的市场驱动因素,以便以后在这些因素上建立盈利的策略。
然而,市场中的相关性和依赖性总是不断变化的,因此,在获取特征重要性时,不仅要追踪过去的平均特征重要性,还要追踪它是如何随着时间的推移而变化的。
本内容仅代表原作者的分析、推测与判断,所依据信息和资料来源于公开渠道,不保证其准确性、充足性或完整性,相关信息仅供参考,不构成广告、销售要约,或交易任何证券、基金或投资产品的建议。本内容中引用的任何实体、品牌、商品等仅作为研究分析对象使用,不代表投资实例和建议。金融交易策略, 特征重要性, 机器学习模型, 数据挖掘

AI时代,拥有个人微信机器人AI助手!AI时代不落人后!
免费ChatGPT问答,办公、写作、生活好得力助手!
搜索微信号aigc666aigc999或上边扫码,即可拥有个人AI助手!